「１」って何だろう？射手座だからこそ「楽しくする」を学ぶ

　こんにちは、かえるさんです。今回は射手座。射手座だからこそ「楽しくする」を学ぶ、と言うお話です。

　「楽しくする」を学ぶ？？「楽しい」の「勉強」なの？

　それを一致させる、と言うことですよ。

　「楽しい」そして「勉強」である、って言うこと？！

　そうです。

　理想的ではあるけれども。

　出来るか、出来ないかで射手座は分かれます、楽しそう、に見えるものだけでなく、奥深さの中に楽しさを見つける、今回はそんなお話です。

「楽しい」＝「ラク」では無い

　射手座と言えば、ワクワクする楽しいこと、やってみなくちゃ判らないことが大好きだよね。

　そうです、射手座は考えることが、とっても好きですから。

　ですから、それを生かして深められれば、すごく役に立ちますし、目の前のことにだけに使うかで、大きく結果が変わります。

　でも、それを言ったら誰でもそうじゃない？

　そうですね、しかし射手座の場合は死活問題ですよ。

　カンタンで楽しいことは、だいたい誰でも好きですよね。

　だいたいじゃなくて誰でも好きでしょ。

　実は、かえるさんは「誰でもカンタンにすぐ出来る」って書いてあると興味を失います。

　何でよ！

　じゃあ、やんなくてもいいや、って思うし、誰でもカンタンにすぐ出来るなら、恐らく役に立たないということでしょう。

　かえるさんも実は、そこそこ射手座は強いのですが、とにかく射手座は話の入り口が大切です。

　面白そう！とか、

　つまんなそう。が大切なんだ。

　だから最初に「つまらなそうだ」と思っても、その気持ちを無視して、最初に頑張れれば、面白くなってきたりするんですよ。それが「楽しそうなこと」しかやらない射手座から「楽しくする」射手座の違いです。

　あー、難しそう、とか、つまんなそう、って思っても、やってみれば深みが判ってきて面白くなるってことか。

　そうです、例えば、仕事ならお金をもらえますよね。そこには、効率化のコツや仕事上の流れでどういう意味を持っているか、じゃあ、こうしよう！などと考え始めれば射手座は楽しめるんですよね。

　ハッキリ言って元から頭は良いんだと思うんだよね、考えっぱなしだし。

　そうなんです。どんなことでも、考えて楽しむコツをつかめば、すごく役に立つんです。

　そこまで頑張れないと、結果にはつながりにくいんだ。

　挫折した時に、挫折を解決する面白さを１度知っちゃえば良いんですよね。でも気が散りやすい欠点もあります。

　そこで頑張れるか、どうかだね。

　ここを越せば絶対面白くなる！って思うか、良く判らねえや。って思うかです。

　だから、最初つまらないと思っても役立つ必要なこと、例えば仕事や勉強なら、楽しくするぞ！、って気持ちが必要なんだ。

　そうです。

「１」「ゼロ」ってなんだろう？

　イメージが悪く、つまらないものの代名詞、算数、数学ですが、実は哲学要素が強い芸術性のある教科です。

　そうなの？

　実際に算数教育の進んだ国では、コンピューターに強い人材が育ちやすく、とても有益な教科ですが、数学なんて社会に出ても役に立たない、などと言う人も多いですね。

　役に立つかね？

　そりゃ、役に立ちますよ。「難しい」って言葉がありますね。どういう意味だと思います？

　理解が困難、複雑、かな。

　そうです、複雑と言うことは、色々な要素が絡み合っているということですね。

　そうだね。

　言いかえれば、分解して１つづつ理解すれば良いわけです。複雑はそうやって克服するのです。

　その手法を練習するために算数、数学はとっても素晴しい教科です。

　だから、大人になって因数分解やサイン、コサインなど忘れてしまっても、それを習得した経験は一生役立ちます。

　「難しい」と言うものがあるんじゃなくて、良く判らない時にそう感じるんだ。

　だからこそ難しいものは判りはじめれば面白いんですね。

　奥深いってことだね。それこそ、射手座向けの一生の楽しみになるんだ。

「１」と「０」のお話

　ちょっぴり「算数」「数学」の哲学的なお話をしましょう。

　にわとりさん、「１」って何でしょう？

　え！「１」は「１」でしょう。

　じゃあ、1つのリンゴを４つに切ります。

　これは「４つ」ですか、「４分の１」が４つですか？

　ええと、いつもは「４つ」って言っているけど、それじゃ増えているみたいになっちゃうから「４分の１」が「４つ」かな。

　でもいつもは「４つ」って言いません？

　言う。「４分の１」とは言わない。

　でも、みんな判りますでしょ、その場に適した表現を自然に使っているわけですね。

　そう言われると、なんでそんな自由なことが許されるんだろう？正確さは求められないのかな。

　でも、元のリンゴからみれば「４分の１」ですが、個別には「１つ」であることには間違い無いでしょ。

　そうか、正確じゃない、とも言えないのか。

　じゃあ「１」をもう少し考えてみましょう。まず「１」は「１」と同じ大きさですね。ですから「１＝１」が成り立ちます。

　そうだね。「１」と「１」は同じ大きさだね。

　では両辺に同じ数をかけたり、同じ数で割っても、同じ大きさですね。

　そうだね。

　両辺を「３」で割ってみます。

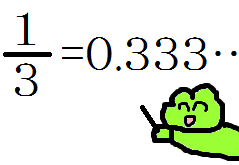
　なるほど、そうだね。

　で、今度は両辺に「３」をかけてみます。

　「３分の１」は「３分の３」になるから約分して「１」だね。

　ですから、こうなります。

　あれ！大きさが違っちゃった！！？？

　いやいや、同じ大きさですよ。

　いや、0.999…の方が少し小さいでしょ。

　同じ操作をしたんですから同じ大きさですよ。

　「１」と「0.999…」は同じ大きさなんです。

　なんか変な気分だな！

　先ほど、にわとりさんは「１」と「１」は同じ大きさだね。と言いましたが、最初のリンゴの話では「１」と「１」は同じではありませんでしたね。

　おー、そう言えば。どうなってんだ？

　一面的には、事実そのものではなく、事実を当てはめることが出来る一つのツールとも言えそうですね。それを踏まえて、事実を伝えるのに大変優れた指標、ツールと言えますね。

　数字って考える余地の無い決まりきったものと思っている人も多いですが、そう言うわけでも無いんです。

　よく漫画や映画で「オレは可能性がゼロになるまで戦うぞ」と言うセリフがありますが、あれは数学では、完全に勝つ可能性が無い、と言う意味ではありません。

　そうなの！？

　数学上は、宝くじの高額当選ほどの小さな可能性ならゼロと言って問題ありません。

　それ言っちゃう。

　逆に言えばゼロとはそういうものなんです。

　え！なんにも無いのがゼロじゃないの？

　何にも無い、って何ですか？

　え！

　例えばこの部屋にリンゴはいくつあるか。なら「ゼロ」とか「１個」等で良いですよね。

　じゃあ、宇宙の誕生、宇宙の一番最初はどうでしょう？

　ああ！何にも無ければ、何も生まれない、でも最初、って聞かれたら、何も無かった、って言うしかない、って話だね。

　そうです、その場合「ゼロ」っていう表現は便利とも言えますね。

　ブラックホールの中心は完全な1点と言うことなのですが、熱が出ている、って問題がありました。

　へー、そうなんだ、どこが不思議なの。

　熱って、振動しているわけですよね。

　あー、そうか、暑いや、熱い、は分子が激しく振動してるんだよね。

　寒い、冷たい、は逆に分子の運動が小さい。

　完全な一点から熱が出るのはおかしいな！何で出るの！

　すごくカンタンに言うと、３次元４次元的には完全な一点ですが、違う次元では面を折りたたんだような状態になっていて面の「部分」が振動していることで熱が出ていると言うことです。

　ぜんぜん判らないけど、そうなんだ。

　でも、そう聞くと「ゼロ」って、色んな使い方があるな。「１」も同じだ。

　数字って哲学でしょ。ただ、数字はあらゆる場面で適切に使うと、情報伝達、説得力に大きな力を発揮します、不確実なもの、ではありませんね。

　でも、なんか不確実と言うか、微妙な所もあるんだね。

　面白いですよね。数字とは何か、を自分なりに考えてみると面白いですよ。

　結局「１」って何！

　そんなの、どんな学者だって困る質問ですよ。今回は「何だろう？」って話ですよ。

　カテゴリー（スマホは画面下のほうです）から、ぜひ他の「語る」「欠点」や「いて座」の記事もごらん下さい～☆

　かえるさんの占いについてはカテゴリー「かえるさんの占い」または画面下の方をごらん下さい～☆